使用 HTML5 绘制三维线框图

虽然我们每个人处在三维的世界中，但是计算机屏幕却是二维的。那么如何将三维的世界展示到二维的屏幕上呢？这时候就需要用到投影。本质上，屏幕上展示的是二维图形，然而二维投影图形会给我们一种视觉上的错觉，大脑经过联想和组合，就会“认为”我们看到了三维物体。

投影是一个数学上的术语，来源于生活。想想看，现在有一个立方体（假设它的表面是可以透光的，并且可以自由旋转），有一束光从立方体上面照下来，为了简化问题，这里只考虑平行光，不考虑点光源的情况（在实际的情况中，灯光在三维世界中很重要，影响着物体被如何渲染）。这样，就在地面上留下了一个影子。类比来说，地面就是计算机的屏幕，影子就是屏幕上绘制的图形，立方体就是实际要表现的东西。当立方体自由旋转时，把每一次的影子记录下来，当立方体全方位旋转后，所有影子组合起来，就完完全全地描述了这个三维的立方体。这种情况被称之为正交投影。

转化

理论知识扯起来很容易，但是如何写出实际的代码就要看手上的功夫了。首先，要描述一个三维物体，需要一些度量值，也就是坐标了。三维物体嘛，当然得有三个坐标，在 JavaScript 中，可以使用数组来表示坐标结构。每一个坐标数组包含了三个元素，代表了空间中的一个点（node）。两个点，就组成了一条线（edge），多条线段就组成了线框图（wireframe）,也就是我想要的效果。三维图形的基础在于点，准确地表达每一个点的坐标非常重要。坐标又是基于坐标系的，所以首先的问题在于明确坐标系。在这个项目，我使用右手系，和canvas绘图标准的坐标系统统一起来：坐标原点在屏幕左上角，X 轴正方向向右，Y 轴正方向向下，Z 轴正方向从内向外。

基础绘制

有了坐标系统，一切都顺风顺水了。在项目中，有一个index.html文件，主要包含了canvas标签，大小是 320X480。然后引用了cube.js文件，这个文件中处理了所有的逻辑。一开始，获取绘图环境，并移动坐标原点到画布中心。

var c = document.getElementById('world');
var ctx = c.getContext('2d');
ctx.translate(160, 240)

然后就是立方体的一大堆描述数据，中心在坐标原点，棱长为 160。

//这是八个顶点
var node0 = [-80, -80, -80];
var node1 = [-80, -80,  80];
...
var node7 = [ 80,  80,  80];
var nodes = [node0, node1, node2, node3, node4, node5, node6, node7];
//连接顶点，形成十二条棱
var edge0  = [0, 1];
var edge1  = [1, 3];
...
var edge11 = [3, 7];
var edges = [edge0, edge1, edge2, edge3, edge4, edge5, edge6, edge7, edge8, edge9, edge10, edge11];

最后把每条棱绘制出来，为了表现效果，着重绘制了每个顶点，并使用不同的颜色区分顶点和棱长。

var draw = function(edges, nodes, texts) {
    ctx.beginPath();
    ...
    ctx.save(); 
    ctx.translate(0.5,0.5); 
    for (var e = 0; e < edges.length; e++) {
        var n0 = edges[e][0];
        var n1 = edges[e][2];
        var node0 = nodes[n0];
        var node1 = nodes[n1];
        ctx.moveTo(node0[0], node0[1]);
        ctx.lineTo(node1[0], node1[1]);
     }
    ctx.stroke();
    ctx.restore();
    ...
}

ctx.stroke是核心的描边方法，在调用此方法前用moveTo与lineTo勾画好路径。在这一步有两个点要注意：第一是绘制之前使用beginPath方法来重新开始新的绘图路径，防止循环调用draw方法时出现残影现象。第二是绘制前先使用save方法保存绘图环境，然后translate(0.5,0.5)偏移 0.5 像素，绘制完成后复原，来缓解canvas的像素模糊效应（出现的原因是canvas绘图时最小的绘制单位是一像素，当使用整数点坐标绘制一像素宽的线段时，线条会被扩展到两个像素宽，使得线段看起来比较模糊）。绘制完成后，用浏览器观察，结果不是很理想：因为屏幕上只有一个正方形而已。其中的原因也很好理解，尽管三维线框图已经被完全绘制在canvas上，但坐标系中的 Z 轴没有被表现出来，只看到 Z 轴方向的投影。小学生都知道正方体的俯视图是正方形，项目已经成功了一半。前言中说过，立方体的假设条件是可以自由旋转。现在就要用到这个条件，开始旋转立方体，时时刻刻绘制正方体的每一次投影，在旋转的时候，角度改变，顶点的位置由原始顶点的投影得到，三角函数派上用场。

旋转起来

简化问题，先考虑绕着 Z 轴旋转的情况。从本质上说，坐标系中的每一个点的坐标就是这个点在坐标轴上的投影位置。

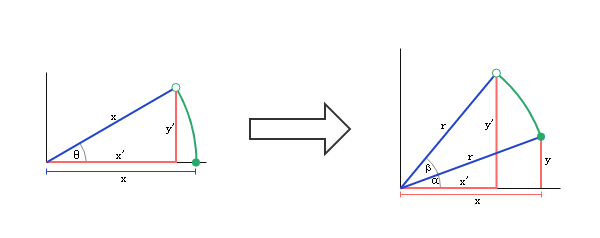初始顶点（x,y）的位置可以用下方的公式一表示：

当绕 Z 轴旋转β角度时，新的顶点(x',y')的位置用公式二表示：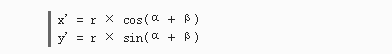

根据脑子里还没忘光的三角公式，可以把公式二展开成公式三：

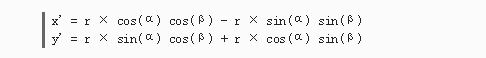将公式一代入公式三，最后得到核心的公式四：

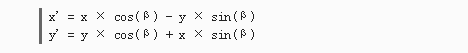有了核心的公式四，把数学语言翻译成编程语言，写到cube.js文件中。

var rotateZ3D = function(theta, nodes) {
    var sin_t = Math.sin(theta);
    var cos_t = Math.cos(theta);
    for (var n = 0; n < nodes.length; n++) {
        var node = nodes[n];
        var x = node[0];
        var y = node[1];
        node[0] = x * cos_t - y * sin_t;
        node[1] = y * cos_t + x * sin_t;
    }
}

X 轴和 Y 轴上的旋转与此类似。接下来的处理很简单，监听鼠标拖动的事件，清空画布ctx.clearRect(-160, -240, 320, 480);，根据拖动的距离和方向设定旋转的角度以及所绕的坐标轴，以此为参数调用旋转方法。更新顶点坐标后，以新的坐标点绘制线框图。为了便于理解，在画布上，我还绘制了坐标轴，在每个点上方添加了数字标识，这些都不是重点，就不一一细说了。

链接

后记

以前觉得所学到的各种高深的数学知识并没有什么用处，完全是为了应付考试才听了一点儿。现在看来，是我太年轻。教育与实践的脱钩让很多学生不能够学以致用。知识其实并不是力量，能够运用知识才是力量，我正在努力挖掘自身的力量。